개요

이론적 배경

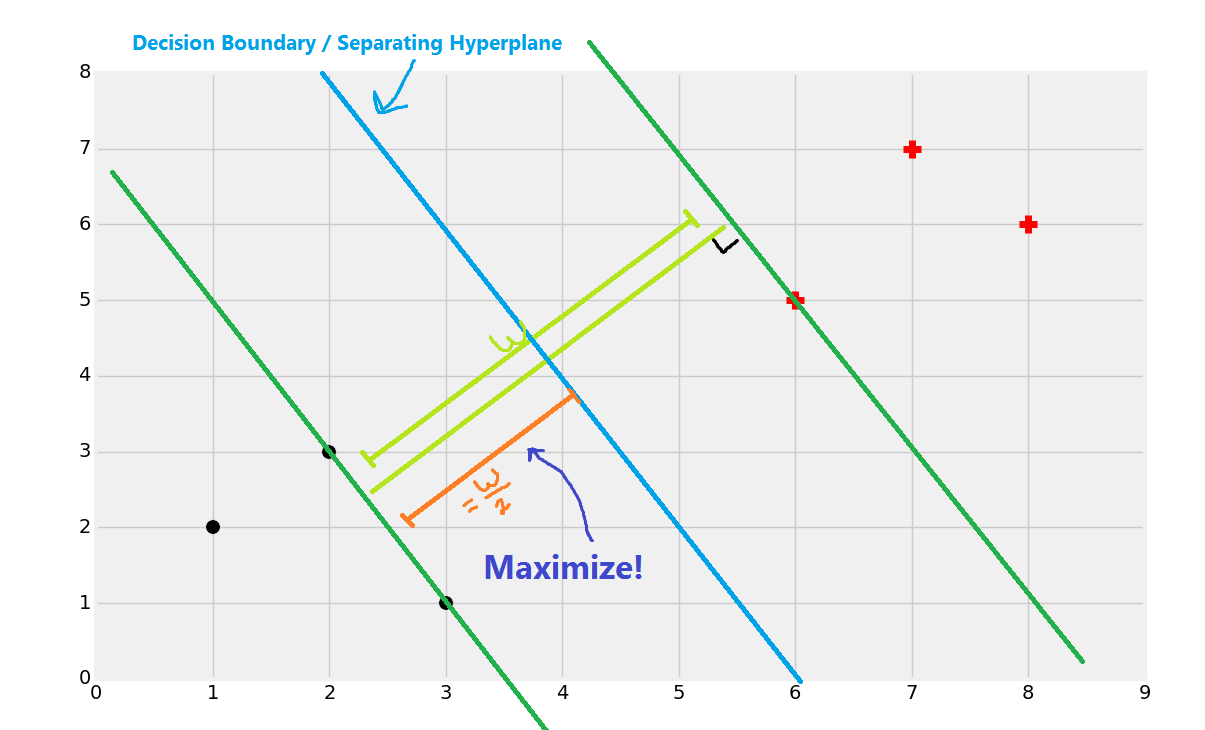
Support Vector Machine은 벡터 스페이스 상에 있는 데이터들을 가장 잘 나눌 수 있는 hyperplane을 찾아내는 것을 목표로 한다. 여기서 핵심은 ‘가장 잘’ 분류한다는 데에 있다.

2차원 평면 상에 두 개의 class를 갖는 데이터포인트들이 존재한다고 가정할 때, 이 점들을 클래스에 따라 나눌 수 있는 직선은 무수히 많이 존재한다. 이 분류 직선(hyperplane)들에 대해 적용하는 기준이 되는 것이 마진(margin)이다.
마진은 hyperplane에 의해 분류된 데이터포인트와 hyperplane 간의 거리들 가운데 가장 짧은 거리를 의미한다.

SVM에서는 마진이 극대화되는 hyperplane을 찾고자 한다.
즉, d차원에서 어떤 데이터 벡터들이 d-1차원의 hyperplane에 의해 분류되었을 때, 이 벡터들 가운데 hyperplane과 가장 가까운 점과 hyperplane 간의 거리가 커질수록 좋은 classfier라고 생각한다는 것이다.

출처: Pratical Machine Learning with Python - Support Vector Machine introduction.

SVM에서 decision boundary를 판단할 때 마진이 클수록 좋다고 생각하는 근거는 모델의 구조적 위험 때문이다.
분류 모형은 모형의 복잡도가 증가할 수록 주어진 학습 데이터를 더 잘 분류할 수 있게 되지만 데이터에 있는 노이즈까지 학습하게 되면서 학습 데이터만 매우 잘 분류하는 모형이 될 위험 또한 커지게 된다.
따라서 어떤 분류 모형이 실제 데이터가 주어졌을 때 이를 잘 분류하기 위해서는 학습 과정에서의 오류를 낮추면서 모델의 복잡도도 줄여야 한다. 이 둘을 합쳐 모형의 구조적 위험이라 한다.

학습 오류(empirical error)와 모형의 복잡도(hypothesis sapce complexitiy)간에는 trade-off 관계가 존재하므로, SVM에서 풀어야 하는 문제는 emperical risk(error)와 hypothesis space complexitiy risk의 합인 모형 전체의 risk 를 최소화하는 것이다.
즉, 구조적 위험의 최소화라는 전체 목표 중에서 데이터 포인트들을 나누는 선들을 구하는 것이 emperical risk problem에 해당하는 것이고, 이렇게 구해진 선들 중 최적해 하나를 찾아내는 것이 hypothesis space risk problem이다.

도출 과정1 (Hard margin SVM, linear case)

Emperical risk는 d차원의 데이터를 나누는 d-1차원의 hyperplane을 구하는 문제로, 아래 수식에서 w와 b를 구하는 것을 의미한다.
w와 b가 정해지면 데이터 포인트들의 x값이 주어질때 아래 수식에 의해 계산되는 각각의 값(상수)는 + 또는 -의 부호를 갖게 되며, 이 부호가 각 데이터포인트들이 속하는 클래스를 의미하게 된다.

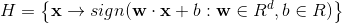
이 수식을 통해 도출되는 w와 b의 조합, 즉 classification boundary는 하나가 아니다.
여러 boundary 가운데 어떤 unique boundary를 고를 것인가는 hypothesis space risk의 최소화 문제가 된다. 이는 곧 모델의 복잡성을 의미하는 VC dimension(이하 h)의 최소화 문제이다.

마진(Δ)과 h 간에는 아래와 같은 관계가 성립한다.

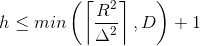
위의 식에서 R은 hyperplane의 반지름으로, 모든 데이터포인트를 감싸는 원을 그렸을 때 그 원의 반지름을 의미한다.
Δ는 hyperplane과 가장 가까운 데이터포인트와의 거리이고, D는 데이터의 차원수이다.
여기서 R와 D는 고정된(주어진) 값이므로 (w,b)로 인해 정의되는 hyperplane에 의해 변동되는 것은 마진(Δ) 뿐이다.
이 식에 따르면 마진이 커진다는 것은 h가 작아진다는 것을 의미하며, SVM의 목표인 같은 classifier라면 모델의 복잡도는 낮을수록 좋다는 것으로 연결된다. SVM이 마진이 최대화되는 분류 hyperplane을 찾는 모델이라는 것은 위와 같은 이유에서이다.

이상의 내용을 수식으로 표현하면 아래와 같다.

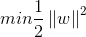
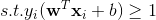
아래의 제약식이 어떤 feature set x의 벡터가 주어졌을 때 이를 + 또는 -로 분류하는 hyperplane을 의미하여, 위의 목적 함수는 제약식을 만족하는 hyperplane 중 마진을 최대화하는 최적값을 찾겠다는 것을 뜻한다.

제약이 있는 최적화 문제를 푸는 것이므로 라그랑주 승수법을 사용할 수 있다. 여기서 α는 Lagrange multiplier이다.

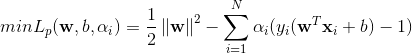
L을 미지수 w와 b로 각각 편미분한 값이 0이 되는 곳에서 최소값을 갖으므로 각각을 정리하면 w와 b를 α와 x, y에 대한 식으로 정리할 수 있다.
이를 상기된 목적 함수에 넣어 정리하면 최종적으로 α, x, y에 대한 식이 나오며, 이 때 x와 y는 이미 주어진 값이므로 SVM의 문제는 미지수 α의 이차방정식을 푸는 문제로 정리할 수 있으며 이는 아래와 같다.

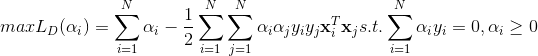
여기서 KKT condition에 따라 아래와 같은 수식이 성립한다.
즉, α가 0이고 y(wx+b)-1이 0이 아니거나, y(wx+b)-1이 0이고 α는 0이 아닌 경우로 나뉘게 된다.

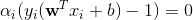
후자의 경우 y(wx+b) = 1을 만족한다는 것은 곧 이 점들이 hyperplane과 가장 가까운 위치에 존재하는 점들로 각 클래스(+, -)의 플러스 평면과 마이너스 평면 상에 위치한다는 것을 의미한다.
이 점들에 대해서만 α는 0이 아닌 값, 정확히 말하면 0보다 큰 값을 가지게 된다. 그리고 0이 아닌 α를 앞선 편미분식에 대입하므로써 w와 b도 구할 수 있다.

정리하면, 마진을 결정하는 데이터 벡터를 사용해 최적화 문제를 해결하는 Lagrange multiplier 및 이를 이용한 w와 b를 구함으로써 SVM에서 찾고자 하는 unique solution인 마진을 최대화 하는 serperating hyperplane을 찾아내는 것이다. 이 때 α가 0이 아닌 벡터들을 일컬어 support vector라고 부른다.

도출과정2 - Soft margin SVM (linear case)

만약 어떤 데이터셋이 hyperplane에 의해 깔끔하게 분류되지 못하는 상황이라면, SVM의 최적화 문제를 곧이곧대로 적용하게 될 경우 데이터가 제대로 분류되지 않거나, 분류되더라도 과적합하는 결과(서포트 벡터에 따라 매우 구불구불한 선)가 나올 수 있다.
이러한 문제를 해소하기 위해서는 기존의 최적화 문제에서 목적 함수를 수정할 필요가 있다.
기본적인 구조는 동일하되, 어떤 데이터 포인트가 마진을 넘는 경우 임의의 패널티를 부여함으로써 약간의 어긋남은 허용해주는 것이다. 이 때 목적함수 및 제약식은 아래와 같다.

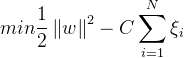
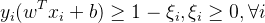
여기서 C는 패널티를 얼마나 과중하게 볼 것인가를 결정하는 파라미터(regularization cost)이다.
이제 목적함수는 마진의 최대화와 페널티의 최소화를 함께 달성해야 한다.

위의 식은 미지수가 3개(w, b, ξ)인 Lagrangian problem이며, 각각의 미지수에 대해 편미분을 수행함으로써 라그랑주 승수 α와 x, y에 대한 식으로 정리하여 푸는 과정은 기존 Hard margin SVM과 동일하다.
이 때 KKT condition에 의해 만족해야 하는 관계는 아래와 같다.

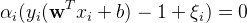
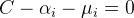
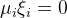
이에 따르면 학습 데이터들은 α = 0 (플러스, 마이너스 평면 밖에 있는 벡터들), 0 ≤ α <C (플러스, 마이너스 평면 상에 있는 서포트 벡터들), α = C (ξ >0 => 상대방 클래스 쪽으로 플러스, 마이너스 평면을 벗어난 벡터들)의 경우로 나뉜다.

앞서 C를 패널티에 대한 파라메터라 하였다. 목적함수에 의하면 패널티의 합계에 곱해지는 C가 커질수록 마진은 작아져야 한다.
이때 C는 0보다 큰 어떤 값이며, SVM으로 데이터를 분류하려는 주체가 결정해야 하는 임의의 값이다.
즉, 0과 무한대 사이에 존재할 수 있는 C에 대해 어떤 값을 적용할지는 grid search를 통해 찾아내야 한다.

Regularization parameter - C & μ

이를 대신하는 새로운 regularization parameter로 제안된 것이 μ이다. (Schölkopf, B., Smola, A., Williamson, R. C., & Bartlett, P. L. (2000). New support vector algorithms. Neural Computation, 12, 1207–1245)
μ-SVM에서 기존의 파라메터 C는 0과 1사이의 범위 내에 존재하는 파라메터 μ로 대체된다.
μ는 C와 달리 하한(0)과 상한(1)이 존재하며 해석이 가능하다.
즉, μ은 전체 학습 데이터에 대한 margin error의 비율의 상한값이자 서포트 벡터의 비율의 하한값을 의미한다.
만약 μ를 0.05의 값으로 설정한다면, 이 SVM은 학습 데이터 중 많아도 5%보다 적은 양의 margin error 벡터를 갖게 될 것이며, 적어도 5%보다 많은 서포트 벡터들을 갖게 될 것이다.

도출과정3 - Soft margin SVM (Non-linear case : Kernel trick)

Soft margin SVM은 약간의 오분류를 허용하지만 본질적으로는 선형 분류기이다.
그러나 데이터의 decision boundary가 비선형이라면 이 방법을 사용하긴 어렵다. 이를 해결하기 위해 사용하는 것이 kernel trick이다.
이는 mapping function을 이용하여 학습 데이터들을 현재 위치하는 차원보다 더 고차원으로 매핑시킨 다음 그 고차원에서 선형 분류를 수행하는 방법이다.

이 방법을 사용하면 기존의 SVM (C-SVM) 최적화 문제에서 제약식 부분의 x가 mapping function을 통해 변환된 ϕ(x)가 된다.
원칙적으로 그 이후의 과정은 기존 프로세스와 동일하다.
다만 여기서 mapping function ϕ()를 찾아야 하는 문제가 발생하는데, SVM에서는 여기서 trick을 사용한다.
즉, 원칙적인 C-SVM의 Lagrangian problem에 의하면 ϕ()에 의해 매핑된 ϕ(x)와 ϕ(x’)의 내적을 계산해야 하는데, 애초에 이 두 argument를 받아 내적값을 게산하는 함수 K(x, x’)를 사용한다면, 매핑 후 내적값을 구하는 것과 동일하다고 볼 수 있다는 것이다.

적용

이상의 내용을 기반으로 kernel trick을 사용한 soft margin SVM에서 regularization parameter로 C를 사용했을 때와 μ를 사용했을 때를 비교해 보자.

Linear Case

Dataset

선형 구분이 가능하나 겹치는 점들이 존재한다.

X_1, y_1 = make_blobs(n_samples=500, centers=2, random_state=0, cluster_std=1.30)
plt.scatter(X_1[:, 0], X_1[:, 1], c=y_1)

X_train, X_test, y_train, y_test = train_test_split(X_1, y_1, test_size=0.30, random_state=2)

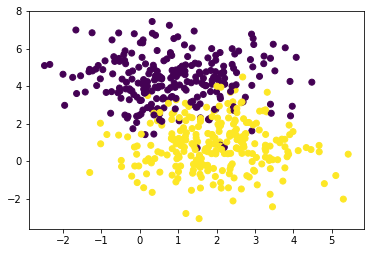
C-SVM (kernel: linear, C=10)

# 이하의 margin plot은 http://scikit-learn.org/stable/auto_examples/svm/plot_separating_hyperplane.html의 코드를 참고하여 작성함.

# fit
model = svm.SVC(kernel='linear',gamma='auto', C=10)
model.fit(X_train, y_train)

# predict
y_pred = model.fit(X_train, y_train).predict(X_test)
con_matrix = metrics.confusion_matrix(y_test, y_pred)
print("-----")
print(con_matrix)
print("-----")
print("Accuracy: {:0.3f}".format(metrics.accuracy_score(y_test, y_pred)))
print("Precision: {:0.3f}".format(metrics.precision_score(y_test, y_pred)))
print("Recall: {:0.3f}".format(metrics.recall_score(y_test, y_pred)))

# plot 
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, s=50)

ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()

xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = model.decision_function(xy).reshape(XX.shape)

ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
           linestyles=['--', '-', '--'])

ax.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1], s=100,
           linewidth=1, facecolors='none', edgecolors='k')
plt.show()

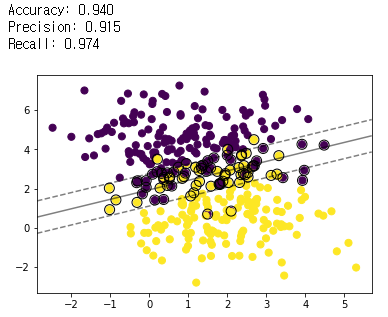
nu-SVM (kernel = linear, nu = 0.5)

# fit
model = svm.NuSVC(kernel='linear',gamma='auto', nu=0.5)
model.fit(X_train, y_train)

# predict
y_pred = model.fit(X_train, y_train).predict(X_test)
con_matrix = metrics.confusion_matrix(y_test, y_pred)
print("-----")
print(con_matrix)
print("-----")
print("Accuracy: {:0.3f}".format(metrics.accuracy_score(y_test, y_pred)))
print("Precision: {:0.3f}".format(metrics.precision_score(y_test, y_pred)))
print("Recall: {:0.3f}".format(metrics.recall_score(y_test, y_pred)))

# plot 
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, s=50)

ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()

xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = model.decision_function(xy).reshape(XX.shape)

ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
           linestyles=['--', '-', '--'])

ax.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1], s=100,
           linewidth=1, facecolors='none', edgecolors='k')
plt.show()

• 동일한 데이터 및 커널(linear)을 사용한 결과 C-SVM에 비해 μ-SVM의 마진이 더 넓게 나타난다.
• 학습 데이터에 대해 테스트 데이터를 사용하여 예측한 결과를 confusion matrix로 만든 뒤 accuracy, precision, recall을 확인한 결과, μ-SVM이 미세하게 높았다.

Paramater tuning with grid search

parameters_c = {'kernel':('linear','poly', 'rbf'), 'C':[0.1, 1, 10, 100]}

model_c = svm.SVC(gamma='auto')
clf_c = GridSearchCV(model_c, parameters_c, cv=5)
clf_c.fit(X_train, y_train)

print(clf_c.best_params_)
print(clf_c.best_score_)

parameters_nu = {'kernel':('linear', 'poly','rbf'), 'nu':[0.1,0.3,0.5,0.9]}

model_nu = svm.NuSVC(gamma='auto')
clf_nu = GridSearchCV(model_nu, parameters_nu, cv=5)
clf_nu.fit(X_train, y_train)

print(clf_nu.best_params_)
print(clf_nu.best_score_)

• SCIKIT-LEARN의 GridSearchCV를 이용하여 C-SVM에서 세 종류의 kernel(Linear, Polynomial, RBF) 및 C값(0.1, 1, 10, 100), μ-SVM에서 동일한 종류의 kernel과 μ값(0.1, 0.3, 0.5, 0.9)에 대한 grid search를 수행하였다.
• 결과 C-SVM에서는 RBF kernel과 C=10, μ-SVM에서는 RBF kernel과 μ=0.3이 최적 파라미터로 도출되었다.

Non-linear case

Dataset

2차원에서 선형 분리가 불가능한 데이터셋을 생성하였다.

X_2, y_2 = make_circles(500, factor=.1, noise=.15)

plt.scatter(X_2[:, 0], X_2[:, 1], c=y_2)

X_train2, X_test2, y_train2, y_test2 = train_test_split(X_2, y_2, test_size=0.30, random_state=2)

C-SVM (kernel = rbf, C=10)

# fit
model2 = SVC(kernel='rbf', gamma='auto', C=10)
model2.fit(X_train2, y_train2)

# predict
y_pred2 = model.fit(X_train2, y_train2).predict(X_test2)
con_matrix = metrics.confusion_matrix(y_test2, y_pred2)
print("-----")
print(con_matrix)
print("-----")
print("Accuracy: {:0.3f}".format(metrics.accuracy_score(y_test2, y_pred2)))
print("Precision: {:0.3f}".format(metrics.precision_score(y_test2, y_pred2)))
print("Recall: {:0.3f}".format(metrics.recall_score(y_test2, y_pred2)))


# plot 
plt.scatter(X_train2[:, 0], X_train2[:, 1], c=y_train2, s=50)

ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()

xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = model2.decision_function(xy).reshape(XX.shape)

plt.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
           linestyles=['--', '-', '--'])

ax.scatter(model2.support_vectors_[:, 0], model2.support_vectors_[:, 1], s=100,
           linewidth=1, facecolors='none', edgecolors='k')
plt.show()

nu-SVM (kernel = rbf, nu = 0.5)

# fit
model2 = svm.NuSVC(kernel='rbf',gamma='auto', nu=0.5)
model2.fit(X_train2, y_train2)

# predict
y_pred2 = model2.fit(X_train2, y_train2).predict(X_test2)
con_matrix = metrics.confusion_matrix(y_test2, y_pred2)
print("-----")
print(con_matrix)
print("-----")
print("Accuracy: {:0.3f}".format(metrics.accuracy_score(y_test2, y_pred2)))
print("Precision: {:0.3f}".format(metrics.precision_score(y_test2, y_pred2)))
print("Recall: {:0.3f}".format(metrics.recall_score(y_test2, y_pred2)))

# plot 
plt.scatter(X_train2[:, 0], X_train2[:, 1], c=y_train2, s=50)

ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()

xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = model2.decision_function(xy).reshape(XX.shape)

ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
           linestyles=['--', '-', '--'])

ax.scatter(model2.support_vectors_[:, 0], model2.support_vectors_[:, 1], s=100,
           linewidth=1, facecolors='none', edgecolors='k')
plt.show()

• Linear case와 동일하게 C-SVM에 비해 μ-SVM의 마진이 더 넓게 나타난다.
• 학습 데이터에 대해 테스트 데이터를 사용하여 예측한 결과를 confusion matrix로 만든 뒤 accuracy, precision, recall을 확인한 결과, μ-SVM이 훨씬 높게 나타났다.

Paramater tuning with grid search

parameters_c = {'kernel':('linear','poly', 'rbf'), 'C':[0.1, 1, 10, 100]}

model_c = svm.SVC(gamma='auto')
clf_c = GridSearchCV(model_c, parameters_c, cv=5)
clf_c.fit(X_train2, y_train2)

print(clf_c.best_params_)
print(clf_c.best_score_)

parameters_nu = {'kernel':('linear', 'poly','rbf'), 'nu':[0.1,0.3,0.5,0.9]}

model_nu = svm.NuSVC(gamma='auto')
clf_nu = GridSearchCV(model_nu, parameters_nu, cv=5)
clf_nu.fit(X_train2, y_train2)

print(clf_nu.best_params_)
print(clf_nu.best_score_)

• 비선형 데이터에 대하여 앞서 선형 데이터애 대한 조건과 동일하게 설정하여 grid search를 수행하였다. (kernel(Linear, Polynomial, RBF), C값(0.1, 1, 10, 100), μ값(0.1, 0.3, 0.5, 0.9)).
• 결과 C-SVM에서는 RBF kernel과 C=100, μ-SVM에서는 RBF kernel과 μ=0.1이 최적 파라미터로 도출되었다.

Parameter 조정 (Case of μ-SVM)

개요에서 선술한 바와 같이, C에 비하여 μ는 한정된 범위(0,1) 내에 존재하며, 값 자체가 해석 가능하다는 특징이 있다. C-SVM에서 C의 값이 변화함에 따라 마진의 크기가 변화하는 것과 마찬가지로 μ의 값의 변화는 마진의 크기 및 서포트벡터의 수를 변화시킨다.

# fit
model2 = svm.NuSVC(kernel='rbf',gamma='auto', nu=0.1)
model2.fit(X_train2, y_train2)

# predict
y_pred2 = model2.fit(X_train2, y_train2).predict(X_test2)
con_matrix = metrics.confusion_matrix(y_test2, y_pred2)
print("-----")
print(con_matrix)
print("-----")
print("Accuracy: {:0.3f}".format(metrics.accuracy_score(y_test2, y_pred2)))
print("Precision: {:0.3f}".format(metrics.precision_score(y_test2, y_pred2)))
print("Recall: {:0.3f}".format(metrics.recall_score(y_test2, y_pred2)))

# plot 
plt.scatter(X_train2[:, 0], X_train2[:, 1], c=y_train2, s=50)

ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()

xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = model2.decision_function(xy).reshape(XX.shape)

ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
           linestyles=['--', '-', '--'])

ax.scatter(model2.support_vectors_[:, 0], model2.support_vectors_[:, 1], s=100,
           linewidth=1, facecolors='none', edgecolors='k')
plt.show()

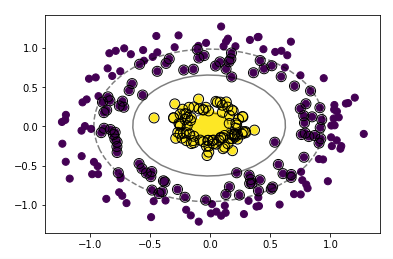
• μ를 0.1로 놓은 SVM과 이전 μ를 0.5로 설정한 SVM을 비교해보면, 0.5 쪽의 마진이 훨씬 넓고 서포트벡터가 많음을 확인할 수 있다.

정리

임의로 만든 2차원 데이터셋에 대하여 C-SVM과 μ-SVM 간에 눈에 띄는 예측력 차이가 발견된 경우는 Non-linear 데이터셋에 대하여 각각 rbf 커널을 적용하였을 때 뿐이었으며 모델링 자체는 문제 없이 수행되었다. 단, 현실 데이터에 약간의 pre-processing을 수행하여 각 모델에 적용하려고 시도해 본 결과 C-SVM은 에러가 발생하지 않았으나, μ-SVM에서는 ‘specified nu is infeasible’라는 에러가 발생하였다. 이는 상술한 바와 같이 μ가 “An upper bound on the fraction of training errors and a lower bound of the fraction of support vectors” ( Scikit-learn nusvc documentation )이므로, 데이터를 fitting하는 과정에서 μ의 지정 범위를 넘어섰기 때문에 발생한 에러이다. 즉, 현실 데이터에 대하여 μ-SVM을 적용하기 위해서는 최적 μ의 탐색과 동시에 모델링에 적합한 데이터셋의 준비가 필요하다.